
Ix is the moment of inertia of the point mass.

k x Sqrt ( I x / m ) Where k x is the radius of gyration. Therefore, the radius of gyration of a body about a given axis may also be defined as the root mean square distance of the various particles of the body from the axis of rotation. The following equation can be used to calculate the radius of gyration. If all the particles are of same mass m, then

Then, the moment of inertia I of the body about the axis of rotation is If we leap to the summing up circular disks of area r2, when we multiply in a factor of r2, we will be weighting each circle of mass according to its radius. Let r 1, r 2, r 3, …, r n be their perpendicular distances from the axis of rotation. Suppose a body consists of n particles each of mass m. In terms of radius of gyration, the moment of inertia of the body of mass M is given as, Simply, gyration is the distribution of the components of an object. This means that if a single mass of `7` kg was placed `2.6` m from the `x`-axis, this would have the same moment of inertia as the original shape when rotating around the `x`-axis.Radius of gyration is defined as the distance from the axis of rotation to a point where the total mass of the body is supposed to be concentrated, so that the moment of inertia about the axis may remain the same. `A=int_1^2 (x^2+1) dx - 1` (We need to subtract the area of the `1xx1=1` square below the shaded area.) We use a computer algebra system to obtain: `x_1= sqrt(y-1)` (the curve closest to the `y`-axis), and `x_2= 2` (the "curve" furthest from the `y`-axis), So the required values which we can use in the formula are: Consider Radius of gyration as ‘K’, Moment of Inertia as ‘I’ and the mass of the body as ‘M’. We take the positive case only, as we are dealing with the first quadrant. Consider a thin circular slice of radius. The radius of gyration represents the distance from a sections centroid at. Since we started with `y=x^2+1`, we solve for `x` and obtain: Moment of inertia of the disc about axis is given by parallel axes theorem is, Hence, the moment of inertia of the cylinder is given as, Solid Sphere a) About its diameter Let us consider a solid sphere of radius and mass. Although the polar moment of inertia can be calculated using the equation. We need to express our function in terms of `y`. In this example, we are rotating the area around the `x`-axis. The moments of inertia had to reference the same axis. The shaded area is the part that's rotating around the `x`-axis, and we have indicated a "typical" rectangle. The moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle. Rotation about the x-axisįor rotation about the x-axis, the moment of inertia formulae become:įind the moment of inertia and the radius of gyration for the area `y=x^2+1` from `x=1` to `x=2`, and `y>1`, when rotated around the x-axis. This means that if a mass of `(2k)/3` was placed `0.447` units from the `y`-axis, this would have the same moment of inertia as the original shape. It's a parabola, passing through (1, 1) and (0, 1). the origin (0,0) of a system which has masses at the points given: MassĪs usual, first we sketch the part of the curve in the first quadrant. Example 1įind the moment of inertia and the radius of gyration w.r.t.
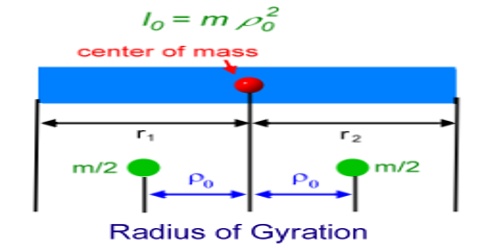
If we wish to place all the masses at the one point ( R units from the point of rotation) thenĭ 1 = d 2 = d 3 =.

d n, (respectively) from the point, then the moment of inertia I is given by: , m n is rotating around a point with distances d 1, d 2, d 3. If a group of particles with masses m 1, m 2, m 3. The moment of inertia of a particle of mass m rotating about a particular point is given by: The moment of inertia is a measure of the resistance of a rotating body to a change in motion.


 0 kommentar(er)
0 kommentar(er)
